Akkoorden en muziektheorie
Om iets meer met muziek te kunnen doen is het erg handig om iets van muziektheorie af te weten. Het volgende stukje probeert zoveel informatie te verstrekken dat termen als toonsoort, tonaliteit, mineur, majeur, akkoorden, akkoordenschema's, intervallen, transponeren, kwintencirkel, een beetje meer inhoud krijgen. Het nu volgende verhaal over toonsoorten, toonladders en akkoorden is verre van compleet; verdergaande informatie kun je vinden in teksten over harmonieleer.
Spelen met muziek
Om muziektheorie wat toegankelijker te maken is het buitengewoon belangrijk dat je kunt horen wat akkoorden bij een melodie doen. Als je uitstekend van blad piano speelt kun je wellicht toe met informatie en voorbeelden op papier (of het web). Als je een niet-akkoordinstrument speelt (alle blaasinstrumenten, viool enz) en/of niet probleemloos van blad speelt is het heel zinvol een bladmuziekprogramma met uitgebreide ondersteuning voor het werken met akkoordsymbolen in te zetten om wat grip op de harmonie te krijgen.
Als in een partij akkoordsymbolen zijn opgenomen dan kun je op basis van de akkoordsymbolen automatisch een aantal begeleidingspartijen laten horen waarvoor de akkoordsymbolen en de maatsoort de basis vormen. Door een (deel van) een muziekstuk in te voeren en met behulp van de hier geboden informatie wat te 'spelen' met akkoorden krijg je al snel meer inzicht in je muziek en zul je er meer plezier aan kunnen beleven.
Afhankelijk van het instrument dat je speelt of waar je partijen voor schrijft zul je rekening moeten houden met de (on)mogelijkheden van het instrument: transpositie en bereik (trompet, klarinet, tuba) akkoordgrepen voor gitaar, ukelele, mandoline, banjo enz.
Je kunt natuurlijk best een contrabaspartij door een sopraanblokfluit laten spelen - andere sleutel en paar octaven omhoog - maar een echt goed idee is dat meestal niet. Als je wat weet van het hoe en waarom van akkoorden zul je veel geschiktere partijen kunnen maken.
Download en installeer (zonder kosten, geen tijdslimiet) en gebruik het programma samen met de hier gegeven informatie om van noten reproduceren via spelen met muziek tot muziek maken te komen.
Muzikale afstanden - veel gebruikte termen
Iedere twee tonen hebben een onderlinge relatie die te maken heeft met de verhouding van hun toonhoogten. In de meeste muziek is de belangrijkste verhouding het octaaf. Het octaaf is de relatie tussen twee tonen waarbij de frequentie van de ene toon precies twee maal zo hoog is als de andere. Op snaarinstrumenten is dit aanschouwelijk te maken door te kijken wat er gebeurt als een snaar met de vingers in twee gelijke delen wordt gedeeld. De toonsafstand tussen de snaar als die in volle lengte klinkt en de snaar als die door een vinger in tweeën is gedeeld is precies een octaaf. Evenzo kan zo'n halve snaar weer in tweeën worden gedeeld, waarmee tussen de halve en de kwart-snaar weer een octaaf zit. Tussen de frequentie van de hele en de kwart-snaar zit dan een relatie van 1:4 dus twee octaven ofwel een dubbeloctaaf.
Muzikale afstanden die in octaven zijn uit te drukken klinken voor ons gehoor eenvoudig. Sterker nog, het is soms moeilijk om te horen of twee tonen nu even hoog zijn (ook wel unisono genoemd) of dat ze een octaafse relatie hebben, zeker als ze door verschillende instrumenten gespeeld worden.
Consonant, dissonant of toch vals...
De mate waarin het oor een muzikale afstand (interval) tussen twee gelijktijdig klinkende tonen als aangenaam ervaart, wordt vaak aangeduid met de term consonant (samenklinkend), terwijl een toonsafstand die "wringt" wordt aangegeven met de term "dissonant" (niet-samenklinkend). "Vals" noemen we intervallen die niet zuiver zijn, d.w.z., geen veelvoud van halve tonen. Onervaren luisteraars zullen dissonant en vals nogal eens verwarren, een interval b-c ofwel een halve toon noemen ze vals terwijl dit alleen zeer dissonant is. In de muziekuitvoering komt een dergelijk dissonant interval vaak voor, terwijl een vals interval (hopelijk) nooit voor komt - experimentele muziek (kwarttonen) en niet-westerse muziek (maqam) even daargelaten.
Muzikale intervallen
In de loop der eeuwen is een muzikale toonschaal ontstaan die het octaaf opdeelt in 12 muzikaal precies even grote stukken, halve tonen genoemd. Een afstand (interval) van twee halve tonen wordt een hele toon genoemd.
Om historische redenen waarover straks bij de behandeling van toonladders meer, hebben ook een aantal andere intervallen een eigen benaming gekregen. De naamgeving is terug te vinden op de piano: begin op de centrale C en ga steeds één witte toets naar rechts. De tweede toets heet dan de secunde, de derde heet terts, gevolgd door kwart, kwint, sext en septiem voor vier t/m zeven.
De termen groot en klein duiden vooral op de eerste terts in de toonladder, grote terts is bijvoorbeeld de afstand tussen de noot c en de noot e (4 halve tonen). Een kleine terts is de afstand tussen de noot c en de noot e♭ (3 halve tonen). Ook voor de septiem wordt veel de benamingen groot of klein gebruikt: de kleine septiem is de afstand c - b♭ (10 halve tonen) terwijl de de grote septiem het interval afstand c - b betreft (11 halve tonen).
De term verminderd duidt op een halve toon verlaging terwijl overmatig en vermeerderd een halve toon verhoging aangeeft.
Een reeks tonen die steeds een halve noot uiteen liggen wordt een chromatische reeks genoemd (wit en zwart op piano), in tegenstelling tot een diatonische reeks zoals de witte toetsen op de piano.

Naamgeving van tonen
Behalve naamgeving voor toonsafstanden is ook naamgeving van toonhoogte ontstaan. Hier zijn een aantal eeuwen geleden zeven letters voor gekozen: A-G. In tijden dat de computer zijn entree nog niet had gemaakt werden octaven aangeduid met 'groot', 'klein' en 'gestreept'. Om mee te rekenen zijn aanduidingen met een octaaf nummer praktischer. Als referentie dient dan meestal de toon A4, ofwel de A boven de centrale C op de piano. Deze A4, de toonhoogte van de meeste stemvorken, heeft meestal een frequentie van 440 Hz (440 trillingen per seconde). Alle andere tonen worden hiervan afgeleid. Een A6 is dus twee octaven hoger dan een A4. De naamgeving van een chromatische reeks is nu als volgt:
- a - a#/b♭ - b - c - c#/d♭ - d - d#/e♭ - e - f - f#/g♭ - g - g#/a♭ - a
Een # achter een letter, en uitgesproken als "-ies", wordt een kruis genoemd en geeft aan dat de toon met een halve noot is verhoogd, terwijl een ♭ (vaak gemakshalve als kleine letter b geschreven), uitgesproken als "-ès" achter een letter een mol wordt genoemd en aangeeft dat de toon met een halve toon moet worden verlaagd. A# wordt ook wel geschreven als Ais terwijl A♭> ook wel als As wordt geschreven. Het valt meteen op dat voor sommige tonen meer dan één benaming wordt gebruikt. Een a# en een b♭ klinken (op piano) hetzelfde maar hebben een verschillende benaming. Het verschil in benaming ontstaat door de functie die een toon binnen een melodie heeft, en wordt enharmonische verwisseling genoemd (op viool hebben ze verschillende hoogte!). Als de toon a#/b♭> fungeert als een verlaagde b, dan wordt deze genoteerd als b♭, en als de functie die van een verhoogde a is dan wordt deze genoteerd als een a#. Ook de doorgaans 'eenvoudig' genoteerde tonen kunnen een alternatieve notatie krijgen; een b die gebruikt wordt als een verlaagde c kan zo als c♭ worden genoteerd, zo ook een als verhoogde b gebruikte c als b#.
Ook kan het soms voorkomen dat in een melodie de toon g# bijvoorbeeld als grondtoon voorkomt terwijl daarnaast ook een verhoogde g# voorkomt. Deze verhoogde g# (dubbelverhoogde g) kan nu geschreven worden als g## (gisis), en klinkt (op een piano) als een a. Om muziek leesbaar te houden zullen dubbelkruisen en mollen niet vaak geschreven worden...

Iedere noot (behalve de g#/a♭) kan in principe dus op drie manieren 'gespeld' worden.
Toonladders
Een toonladder vormt de basis van iedere melodie (a-tonale muziek buiten beschouwing gelaten). Uitgaande van een zich na een octaaf steeds herhalende toonladder delen we het octaaf weer in een aantal stukken. Vanwege de voorkeur van ons oor voor consonante verhoudingen is een reeks van acht noten ontstaan die er als volgt uitziet:
- Priem, Secunde, Terts, Kwart, Kwint, Sext, Septiem, octaaf,
ofwel de namen voor 1e t/m 8e in het Latijn. Een dergelijke reeks tonen wordt een diatonische toonladder genoemd vanwege het ontbreken van een aantal (halve) tonen. Iedere toon van die toonladder heeft zodoende een vaste relatie met de eerste toon van die toonladder, vaak aangegeven met de hiervoor genoemde naam in het Latijn.
Als voorbeeld nemen we de toonladder van C: c-d-e-f-g-a-b-c. Op de piano komt dit neer op 8 naast elkaar liggende witte toetsen vanaf C. Het notenbeeld ziet er uit als in de figuur hierna.

c d e f g a b c
Tot zover tamelijk rechttoe-rechtaan, maar hoe gaat het nu als je niet op de c begint maar op een a?
a-b-c-d-e-f-g-a heeft als toonladder een heel ander karakter dan c-d-e-f-g-a-b-c hoewel ze gebruik maken van precies dezelfde noten. Het verschil zit hem in de afstanden, hoewel je dat op een notenbalk eigenlijk niet eens ziet:

a b c d e f g a
Steeds zit tussen de B en C resp. E en F een toonsafstand van een halve toon terwijl tussen alle andere een afstand van een hele toon aanwezig is. Niet alle sporten van de ladder zijn even groot! De eerste toonladder wordt een majeur toonladder genoemd, de tweede een mineur-toonladder. Ook op de andere tonen kan een toonladder worden gebouwd, alleen klinken de meeste ons vreemd in de oren. Wat nu als we het karakter van de toonladder willen behouden, maar alles een hele noot hoger willen laten klinken. Wat er moet gebeuren is het gelijk houden van de afstanden zoals bij de beschreven toonladder van C. Hiervoor moeten de F en C met een halve toon verhoogd worden, en we krijgen nu een toonladder met twee kruisen. In het notenschrift worden deze kruisen vooraan bij iedere regel genoteerd om aan te geven dat ze eigen zijn aan de toonladder in tegenstelling tot noten die in een melodie toevallig verhoogd/verlaagd worden, welke toonladder-vreemd heten.
d e f# g a b c# d
Steeds zal in een majeur toonladder de afstand tussen de 3e en de 4e traptrede van de ladder, en die tussen de 7e en 8e trap een halve toon zijn terwijl die tussen de ander traptreden een hele is.
Laten we nu eens de mineur toonladder van D gaan vergelijken met de majeur toonladder van D:

d e f# g a b c# d
- D-groot (majeur)
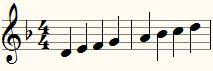
d e f g a b♭ c d
- D-klein (mineur)
Beide notenbeelden zien er (op de voortekens na) precies hetzelfde uit, maar klinken heel anders!
Laten we maar eens kijken naar afstanden tussen de noten. Het eerste dat opvalt is het verschil in afstand tussen de grondtoon en de derde trap. Voor de majeur toonladder zijn dat twee hele tonen, terwijl dat voor de mineur toonladder een hele plus een halve toon is. Men zegt nu dat de afstand van de eerste tot derde trap een grote terts is voor de majeur- of grote-terts toonladder, terwijl die bij de mineur-toonladder een kleine-terts is, en dus ook wel kleine-terts-toonladder wordt genoemd.
Bij iedere toonladder horen dus een aantal mollen of kruisen; behalve bij de toonladders van C-majeur en A-mineur (Am) die zonder kruisen of mollen geschreven worden. De toonladder van A-mineur en C-majeur worden vanwege gelijke voortekens wel elkaars parallel genoemd, A-mineur is dus de parallelle mineurtoonladder van C-majeur. Hetzelfde geldt voor bijvoorbeeld D-mineur en F-majeur, beiden met een mol. Zo hoort bij elk van de twaalf majeurtoonladders steeds een parallelle mineurladder die een kleine terts lager begint. Parallelle toonladders worden vaak binnen een melodie door elkaar gebruikt.
Akkoorden
Akkoorden zijn in hun simpelste vorm drieklanken en bestaan dus ook uit minimaal drie noten die tegelijkertijd te horen zijn. Een melodie kan meestal op eenvoudige wijze worden begeleid door akkoorden. Vanuit de akkoorden kan dan weer een bas-partij worden gevonden, tweede stemmen enz.
Majeur
Akkoorden en toonladders hebben een heel directe relatie; uit de gebruikte toonladder volgen vaak meteen de te gebruiken akkoorden en andersom. Als we nog een keer de toonladder van C-majeur ten tonele voeren kunnen we eens kijken hoe drieklanken in die toonladder terug te vinden zijn. Om lekker te klinken in een toonsoort moet een drieklank opgebouwd worden uit tonen die in de toonladder voorkomen ofwel laddereigen zijn. Een tweede beperking die we vinden voor makkelijk in het gehoor liggende akkoorden is dat akkoordnoten niet naast elkaar mogen liggen.
Door op iedere trap(trede) van de toonladder een drieklank te bouwen (steeds één trede overslaan) vinden we 7 drieklanken, die we nu aangeven met een Romeins cijfer voor de trap (-trede van de toonladder) waarop het akkoord is begonnen (relatieve akkoordnotatie ten opzichte van de toonsoort). De gevonden drieklanken hebben echter niet alle hetzelfde karakter: op I IV en V klinken de akkoorden groot (majeur), ze zijn opgebouwd uit een grote terts met daar bovenop gestapeld een kleine terts. Dergelijke majeur akkoorden worden vaak bij muziek genoteerd met hoofdletters: C F en G voor I IV en V in C-groot (akkoorden in letters onafhankelijk van de toonsoort).

Op II III en VI kunnen we drie klein (mineur) akkoorden vinden, een kleine terts met daar bovenop een grote terts. Mineur akkoorden worden genoteerd met de als hoofdletter de grondtoon van het akkoord gevolgd door een kleine letter m. Am, Em en Dm voor resp. VI, III en II in C-groot.
Eén akkoord hoort in geen van beide categorieën: op VII zit een verminderd akkoord, opgebouwd uit twee kleine tertsen. Verminderde akkoorden worden genoteerd met de letter van het akkoord gevolgd door een klein nulletje iets hoger: Bo of ook wel als Bdim. Ze komen veel minder voor dan de mineur en majeur akkoorden en laten we voor nu even buiten beschouwing.
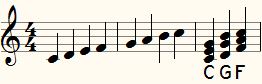
Het valt na enig koekeloeren naar bovenstaande akkoorden op dat met de drie majeur akkoorden C G en F de hele toonladder als het ware bedekt kan worden. Hetzelfde geldt ook voor de drie mineur akkoorden Am Em en Dm. Het lijkt voor de hand te liggen om melodieën te begeleiden met een set van drie akkoorden zoals hier beschreven.
Behalve uit drie, kunnen akkoorden ook uit vier of meer verschillende noten bestaan (noten die een octaaf uit elkaar liggen beschouwen we hier als 'gelijk'). Er is echter maar één zo'n akkoord dat ook nog erg goed in het gehoor ligt. Als we het nog ongebruikte VII akkoord combineren met het V akkoord ontstaat wat men een septiem-akkoord noemt en wordt genoteerd als G7 omdat de extra f in dit akkoord de (verlaagde) zevende noot uit de toonladder van G is (verlaagd want in de toonladder van G zit normaliter een f# en geen f).
Wat is nu de lol van een dergelijk septiem-akkoord? Het blijkt dat zo'n septiem-akkoord als dat ten gehore wordt gebracht 'spanning' oproept, een vraag stelt, die kan worden opgelost door een ander akkoord er achteraan te spelen. Het akkoord dat de vraag het best beantwoordt van de ter beschikking staande 7 mogelijkheden is het akkoord op de grondtoon, in dit geval het C-akkoord.
Nog even wat kretologie, de akkoorden op de trappen hebben nog alternatieve veel gebruikte functionele benamingen:
| I | Tonica |
| II | Supertonica |
| III | Mediant |
| IV | Subdominant |
| V | Dominant |
| VI | Submediant |
| VII | Subtonica |
Mineur
Bij mineurtoonladders treedt een complicatie van ons verder toch redelijk eenvoudig modelletje van de harmonieleer waar we in feite mee bezig zijn. Wat is het probleem?
Voor een majeur toonladder hadden we twee akkoorden gevonden die heel sterk met elkaar waren verbonden: het dominant-septiem akkoord dat als het ware om het tonica-akkoord vraagt.
Maar waardoor ontstaat dat vraag-effect nu. Het blijkt dat halve-noot-afstanden een sterke aantrekking uitoefenen. In de majeur-toonladder is op de derde en zevende trap een halve-toonsafstand aanwezig. Bij de akkoord overgang van G7 naar C worden beide halve-toonsafstanden gebruikt; f→e en b→c
Als we de mineur toonladder er eens bij zetten en ook de akkoorden op I V7 en IV bewonderen dan vinden we Am, Em7 en Dm. We zijn nu helaas bij de overgang Em7 naar Am wel een halve-toons-sprong kwijtgeraakt, terwijl de overgebleven b→c lang zo effectief niet trekt; in C-groot trok die overgang sterk naar de tonica terwijl dat in A-klein niet het geval is (de noot c is hier immers niet de grondtoon...).

We kunnen hier wel iets aan doen, en daarmee introduceren we meteen een nieuw soort toonladder. Als we in plaats van de 'gewone' zevende trap een verhoogde zevende trap in de toonladder nemen (een g# in plaats van een g) dan creëren we daarmee een extra halve toonsafstand g#→a, jawel de 'trekker' waar we om verlegen zaten. De prijs die we daarvoor betalen is een toonsafstand van anderhalve toon tussen f en g#. Dit kan soms wel wat exotisch klinken. De toonladder wordt de harmonisch mineur toonladder genoemd.

Een remedie voor die anderhalve toon is het eveneens verhogen van de 6e trap. Dat zou betekenen dat het subdominant-akkoord ook majeur zou worden... De uiteindelijke remedie voor dit dilemma is het verhogen van VI en VII "indien nodig" dus als een overgang E7 → Am plaats vindt: de zo ontstane toonladder wordt meestal aangeduid onder de naam melodische mineur toonladder: stijgend met f# g#, dalend met g f.

We zijn tot de majeur en mineur toonladder gekomen door op de witte toetsen van de piano te beginnen op respectievelijk de c en de a, met heel verschillend klinkende toonladders tot gevolg. Zo kun je op iedere ander noot ook beginnen: en krijg je de kerktoonladders. Een daarvan die regelmatig voorkomt is de ladder die begint op een d. Ter vergelijking met de eerdere toonladders even naar a getransponeerd, levert dat de dorische mineurladder op:

Een heel bekend voorbeeld van een muziekje in een dorische ladder is bijvoorbeeld "The drunken sailor". De cruciale verschillen in karakter tussen de verschillende toonladders worden veroorzaakt door de plaats van de halve toonsafstanden in de ladders.
De kwintencirkel
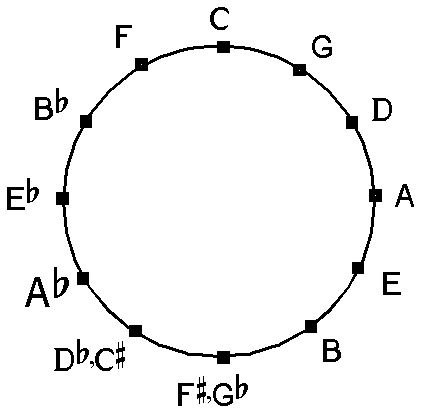
Met de zogeheten kwintencirkel kunnen een groot aantal muziektheoretische zaken in een handzaam kader geplaatst worden. Leuk, maar wat is dat nou...
Als je begint bij een C en steeds een kwint (=7 halve tonen) hoger gaat krijg je de volgende reeks:
c - g - d - a - e - b - f# - c# -g# - e♭ - b♭ - f - c
Met de C in het midden krijgen we met erboven het aantal kruisen of mollen dat bij de corresponderende majeur en mineur toonsoorten horen:
| kruisen/mollen | 7♭ | 6♭ | 5♭ | 4♭ | 3♭ | 2♭ | 1♭ | - | 1# | 2# | 3# | 4# | 5# | 6# | 7# |
| majeur | C♭ | G♭ | D♭ | A♭ | E♭ | B♭ | F | C | G | D | A | E | B | F# | C# |
| mineur | A♭m | E♭m | B♭m | Fm | Cm | Gm | Dm | Am | Em | Bm | F#m | C#m | G#m | D#m | A#m |
Het valt nu meteen op dat bij mineur en majeur toonladders met gelijke grondtoon (C en Cm bijvoorbeeld) drie mollen meer/kruisen minder genoteerd moeten worden.
Omdat de f# en g♭ op piano hetzelfde zijn kan deze reeks ook in de vorm van een cirkel worden getekend: de kwintencirkel.
Als de C bovenin staat, dan staat iedere stap in klokrichting voor één kruis voor de toonladder erbij of een mol eraf, terwijl iedere stap tegen de klokrichting in staat voor een kruis eraf of een mol erbij. De toonladder van E♭-groot heeft dus 3 mollen, die van B-groot 5 kruisen (enz.)
Akkoorden vinden bij een melodie.
Het vinden van akkoorden bij een melodie vereist enige oefening en vooral goede oren! Hier volgen een paar 'hints' om snel akkoorden bij een gegeven melodie te vinden.
1) Achterhaal in welke toonsoort de melodie staat (of moet staan). De meest voor de hand liggende mogelijkheid is de noot waarmee de melodie begint en/of eindigt (ca. 75% kans). In geval van een opmaat: kijk naar de eerste noot van de eerste echte maat.
2) Bepaal of de melodie een mineur ('droevig') of majeur ('vrolijk') karakter heeft.
3) Als in 1) bijvoorbeeld een G werd gevonden en in 2) droevig, dan is de toonsoort dus G-mineur (Gm) en heeft dus (zoals te vinden in het voorgaande tabelletje) twee mollen als voorteken. Evenzo A en vrolijk geeft A-majeur (A) en dus 3 kruisen vooraan de balk.
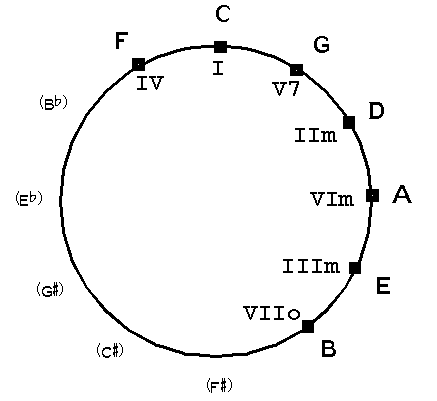
4) De toonsoort bepaalt nu voor een groot deel welke akkoorden gebruikt kunnen worden. We hadden al gezien welke akkoorden het meest voor de hand liggen in een toonladder namelijk: I, V7 en IV. We kunnen deze makkelijk terugvinden met behulp van de kwintencirkel. Kijk op de kwintencirkel naar de tonen die links en rechts van de grondtoon van de toonladder staan. Dit zijn precies het IV, I en V akkoord met het akkoord dat dezelfde naam heeft als de toonladder in het midden. Het meest gebruikte akkoord is het tonica-akkoord ofwel het akkoord dat dezelfde naam heeft als de toonladder zelf. Het tweede belangrijke akkoord is het akkoord dat op de kwintencirkel rechts naast de tonica staat. Dit akkoord wordt dominant akkoord genoemd omdat dit de toonladder domineert. Het dominant-septiem akkoord is ook het enige majeur akkoord dat met septiem laddereigen is. Voor C-groot hebben we zodoende als akkoorden:
C G7 en F als basis en Am Em Dm (en BØ) ter afwisseling. In MusiCAD kun je de akkoordassistent gebruiken om te helpen bij het uitzoeken van de begeleidingsakkoorden.
5) Begin het begeleiden van een melodie met het akkoord op de tonica. Als dit niet meer klinkt, probeer dan het dominant (of dominant septiem akkoord). Als ook dit niet klinkt, probeer dan het sub-dominant akkoord (in C-groot worden dit dus resp.: C G7 en F, of in A-klein Am E7 en Dm.)
6) Als een I-V7-IV begeleiding niet voldoet kun je met behulp van de kwintencirkel nog wat extra mogelijke akkoorden vinden; rechts naast het IV-I-V7 trio staan nog IIm, VIm en IIIm of III7 ter beschikking. In de afgebeelde kwintencirkel is de tonica (=I) C. De toonladder is op de cirkel gemarkeerd.
Voor andere toonsoorten dan C (resp. Am) kan de inhoud van de kwintencirkel als het ware gedraaid worden om de juiste akkoorden te vinden: zorg dat I bij de toonsoort staat, en alle bij de toonsoort behorende akkoorden zijn af te lezen.
| IV | I | V7 | IIm | VIm | IIIm | VIIØ | ||
| Es-majeur | ♭♭♭ | A♭ | E♭ | B♭7 | Fm | Cm | Gm | DØ |
| Bes-majeur | ♭♭ | E♭ | B♭ | F7 | Cm | Gm | Dm | AØ |
| F-majeur | ♭ | B♭ | F | C7 | Gm | Dm | Am | EØ |
| C-majeur | F | C | G7 | Dm | Am | Em | BØ | |
| G-majeur | # | C | G | D7 | Am | Em | Bm | F#Ø |
| D-majeur | ## | G | D | A7 | Em | Bm | F#m | C#Ø |
| A-majeur | ### | D | A | E7 | Bm | F#m | C#m | G#Ø |
| IVm | Im | V7 | IIØ | VI | III | VII | ||
| C-mineur | ♭♭♭ | Fm | Cm | G7 | DØ | A♭ | E♭ | B♭7 |
| G-mineur | ♭♭ | Cm | Gm | D7 | AØ | E♭ | B♭ | F7 |
| D-mineur | ♭ | Gm | Dm | A7 | EØ | B♭ | F | C7 |
| A-mineur | Dm | Am | E7 | BØ | F | C | G7 | |
| E-mineur | # | Am | Em | B7 | F#Ø | C | G | D7 |
| B-mineur | ## | Em | Bm | F#7 | C#Ø | G | D | A7 |
| Fis-mineur | ### | Bm | F#m | C#7 | G#Ø | D | A | E7 |
Eén van de belangrijkste dingen om van dit verhaal over toonladders te onthouden is: halve toonsafstanden trekken. Als je in een melodie (of tweede stem) op de juiste plaatsen halve toonsafstanden gebruikt (en de daarbij behorende akkoorden), trek je de melodie als het ware 'vooruit'. In de kwintencirkel vind je de halve toonsafstanden steeds terug op de derde en zevende trap van ieder septiemakkoord.

Speel maar eens B7 - E7 - A7 - D7 - G7 - C, - een stukje van de kwintencirkel - en je hoort een heel dwingende reeks van steeds halve toonsafstanden.
In zo'n reeks septiemakkoorden kun je bij iedere akkoordovergang zelfs een derde halve toonsafstand vinden bijv. bij B7-E7 is er behalve d#-d en a-g# ook nog d#-e te beluisteren. In de slotovergang G7-C laat je nu het septiem (de B♭) weg, waardoor de dwang naar weer een volgend akkoord wegblijft; we zijn weer thuis (in de veronderstelling dat we in C-groot spelen).
Notatie en gebruik van 'moeilijke' akkoorden.
Na het voorgaande verhaal zullen veel akkoordpartijen hopelijk wat duidelijker geworden zijn. Als je door bladmuziek waarin akkoordsymbolen gebruikt worden bladert, dan zul je merken dat er nogal eens wat ingewikkelder akkoorden gebruikt worden zoals C6, C9, C+, CØ,Co, Csus4, CmΔ enz. Als je eenmaal weet hoe de standaardakkoorden opgebouwd zijn, dan is het niet zo moeilijk om te achterhalen hoe de uitgebreide akkoorden in elkaar steken.
In het eerdere verhaal heb je gemerkt dat de nadruk heel sterk heeft gelegen op toonladdereigen akkoorden. Als laddereigen drieklanken (akkoorden met drie tonen) heb je drie typen akkoord gezien:
- majeur: grote terts + kleine terts ( C: c-e-g )
- mineur: kleine terts + grote terts ( Cm: c-e♭-g )
- verminderd: twee kleine tertsen: ( C° of Cdim: c-e♭-g♭ )
Als overblijvende mogelijkheid is er nog:
- vermeerderd: twee grote tertsen ( C+ of Caug: c-e-g# )
Van belang zijn nog een drietal buitenbeentjes (niet bestaand uit grote of kleine tertsen):
- hardverminderd: grote terts+verlaagde 5 (C-, C(♭5) C(-5) : c-e-g♭)
- voorhouding: hardverlaagde 3: (C2 of Csus2: c-e♭♭-g ofwel c-d-g )
- voorhouding: verhoogde grote terts: (C4 of Csus4: c-e#-g ofwel c-f-g)
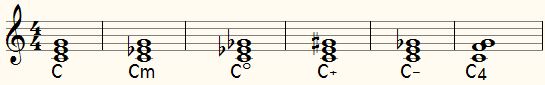
Als je de nu bekende drieklanken gaat uitbreiden met een extra terts krijg je de septiemakkoorden, waarvan de belangrijkste zijn:
uitbreiding met kleine terts
| C7 | c-e-g-b♭ | dominant-septiem | |
| Cm7 | c-e♭-g-b♭ | mineur-septiem | |
| C° | c-e♭-g♭-b♭♭ | verminderd-septiem | (ook C°7, Cdim, Cdim7) |
Die laatste noot uit het verminderd-septiemakkoord (de b♭♭, beses dubbelverlaagde b) wordt vaak als a herschreven - waarmee de tertsafstand wat onduidelijk naar voren komt: het interval ziet er niet meer uit als terts g♭ - b♭♭ maar als overmatige secunde g♭-a. Meestal wordt er toch maar een een a genoteerd om lastig leesbare dubbelverlagingen te vermijden die op veel instrumenten toch geen andere speelwijze tot gevolg hebben.
Uitbreiding met grote terts
| CΔ | c-e-g-b | groot-septiem | (ook CM7, CMaj7) |
| CmΔ | c-e♭-g-b | mineur-groot-septiem | (ook CmM7, CmMaj7) |
| Cø | c-e♭-g♭-b♭ | halfverminderd-septiem | (ook Cm7(♭5)) |

Nog een terts erbij geeft de zogeheten none-akkkoorden:
| C9 | c-e-g-b♭-d | dominant-none |
| Cm9 | c-e♭-g-b♭-d | mineur-none |
Merk op dat het doorstapelen op een verminderd-septiemakkoord geen 'nieuw' akkoord oplevert; de grondtoon komt er nogmaals bij. Verder doorstapelen van tertsen geeft achtereenvolgens "undecime"; (of in gewoon Nederlands "elf") en "tredecime"; ("dertien") akkoorden, waarvan de meest gebruikelijke zijn:
| Cm11 | c-e♭-g-b♭-d-f# | mineur-elf |
| C13 | c-e-g-b♭-d-f#-a | dertien |
Als je in dit laatste akkoord de extra tertsen behalve de laatste weglaat krijg je een akkoord dat meestal aangeduid wordt als zes-akkoord (de 'dertien' een octaaf naar beneden levert een 'zes').
| C6 | c-e-g-a | zes |
| Cm6 | c-e♭-g-a | mineur-zes |
Deze laatste twee (vaak laddereigen) akkoorden worden vrij veel gebruikt. Ook het weglaten van noten gebeurt veel; een C9 wordt vaak als c-e-g-d gespeeld.

We hadden al gezien dat gemakshalve losse noten enharmonisch verwisseld kunnen worden. Ook bij akkoorden kan iets dergelijks gebeuren. Met evenveel recht kan een akkoord bestaande uit g#-b-d-f een G#°-akkoord genoemd worden als een A♭° akkoord (g# = a♭) Bij deze verminderd-septiem akkoorden is nog meer aan de hand. Een B° akkoord bestaat uit b-d-f-g# en dus uit dezelfde noten als G#°. Ook D° en F° zijn enharmonische verwisselingen van dit zelfde akkoord.
In feite bestaan er maar drie wezenlijk verschillende verminderd-septiem akkoorden:
| C° | = | E♭° | = | F#° | = | A° | ook D#° resp. G♭° |
| C#° | = | E° | = | G° | = | A#° | ook D♭° resp. B♭° |
| D° | = | F° | = | G#° | = | B° | ook A♭° |
Iets dergelijks kun je aantreffen bij de vermeerderde of overmatige (augmented) akkoorden:
| C+ | = | E+ | = | G#+ |
| C#+ | = | F+ | = | A+ |
| D+ | = | F#+ | = | A#+ |
| E♭+ | = | G+ | = | B+ |
Dan zijn er nog akkoorden die in een andere ligging ineens een ander akkoord vormen:
| I6 | = | VIm7 | : | C6 | : | c-e-g-a | = | Am7 | : | a-c-e-g |
| IIm6 | = | VIIØ | : | Dm6 | : | d-f-a-b | = | BØ | : | b-d-f-a |
Een akkoordenvoorbeeld

Het bovenstaande stukje is hier voorzien van een heleboel akkoorden. Met de regels zoals we die eerder hadden opgezet zouden het er veel minder geworden zijn. C | G7 | G7 | C | C | G7 | G7| C | had ook gekund.
In akkoordschema's zoals ze in de praktijk gebruikt worden is de beperking dat akkoorden laddereigen moeten zijn meestal niet strikt van toepassing. Het op de juiste plaats gebruiken van laddervreemde akkoorden kan juist de sfeer oproepen die je nodig hebt bij het arrangeren van een melodie.
verminderd ° dim dim7
Verminderde akkoorden kun je vaak als 'doorgangsakkoord' gebruiken; in het volgende stukje wordt steeds een verminderd akkoord gebruikt om een hele noot in je akkoordlijn omhoog te gaan. Je wilt van C naar Dm, het C#° akkoord kun je nu als tussenstation gebruiken. G naar Am dito met G#°, evenals F naar G met het F#° akkoord eveneens. De verminderde akkoorden kun je makkelijk inruilen voor een ander verminderd akkoord: C#° c#-e-g-b♭ en laat zich probleemloos verwisselen met E°, G° of B♭°. Verminderde akkoorden zijn doorgaans niet laddereigen, behalve in een harmonisch mineur ladder, bijvoorbeeld in A-klein-harmonisch op de tweede trap: b-d-f-a♭ als je de a♭ inruilt voor een g#
halfverminderd Ø m7(b5)
Halfverminderde akkoorden kunnen laddereigen zijn: BØ b-d-f-a is laddereigen in C-groot en A-klein. Een halfverminderd akkoord is enharmonisch verwisselbaar met het mineur-6 akkoord van de terts: Dm6 d-f-a-b.
vermeerderd +
Een vermeerderd (ook wel overmatig) akkoord kan in de majeur toonladder nooit laddereigen zijn; geen van de majeur akkoorden is in de toonladder vermeerderd te maken. Bijv. in C groot: C+ krijgt een laddervreemde g#, G+ krijgt een d#, en F+ een c#. Wanneer kun je zo'n vermeerderd akkoord dan gebruiken? Dit kan bijvoorbeeld als vervanging van het dominant-septiemakkoord (mits de melodie e.e.a. toelaat.) Doorgaans gebruik je om van G naar C te gaan het G7 akkoord met als trekkende noten de b (naar c) en de f (naar e). Met een G+ akkoord kan het ook; de laddervreemde d# trekt naar de laddereigen e. De vermeerderde akkoorden laten zich vervangen door twee andere vermeerderde akkoorden: C+ c-e-g# met E+ en G#+
groot-septiem Δ, Δ7, Maj, M7, Maj7
Het gebruik van groot-septiem akkoorden heeft vaak als gevolg dat de harmonie als het ware blijft 'zweven'. De aanwezigheid van zowel een c als een b in bijvoorbeeld een CΔ lijken elkaars effect op te heffen. De c wil (in de toonladder) naar b. De b naar c. Met andere woorden, ook al wordt aan het verzoek voldaan, dan nog is de spanning niet verdwenen. Merk op dat zowel op I als op IV een laddereigen groot-septiem akkoord te gebruiken is (in C: CΔ en FΔ). Mineur groot-septiem akkoorden zijn meestal niet laddereigen; alleen AmΔ is laddereigen in Am in melodische/harmonische variant. In de oorspronkelijke mineurtoonladder (zonder verhoogde septiem) zijn alle mineur groot-septiem-akkoorden laddervreemd.
Omkeringen

Akkoorden kun je in verschillende 'ligging' spelen, immers een C-akkoord bestaat uit c-e-g en kun je als c-e-g (grondligging), e-g-c en g-c-e spelen. Met name ingewikkelder akkoorden klinken niet in alle liggingen even bruikbaar; de noten die je wilt laten opvallen kunnen het beste zo hoog mogelijk in het akkoord liggen. C7 gespeeld als b♭-c-e-g 'wringt' meer dan c-e-g-b♭ (vanwege de secunde b♭-c) het laatste lost ook nadrukkelijker op naar F: c-f-a beide leidtonen e-f en b♭-a liggen zo hoog mogelijk.
c-e-g-b♭ naar f-a-c is veel minder nadrukkelijk.
Veel voorkomende akkoordenschema's
Een paar veel voorkomende akkoordenschema's, alles in C resp. Am:
| C F G7 C | (slot) cadens (I-IV-V7-I) |
| Am Dm E7 Am | idem mineur (Im-IVm-V7-Im) |
| C G F C | plagale cadens (IV-I i.p.v. V-I als slotakkoorden) |
| Am E7 A | picardische terts (Im-V7-I) |
| C Dm G7 C | authentieke cadens (I-IIm-V7-I) |
| Am G F E7 | Andalusische cadens (Im VII VI V7) |
| C D7 G7 C | tussendominant (uitstapje naar hoger gelegen toonsoort) |
| Am B7 E7 Am | idem mineur. |
| C F Fm C | mineur IV (laddervreemd) |
| C C7 A A7 Dm G7 C | majeur III |
| C C#o Dm | doorgangsakkoord (halve tonen in de bas) |
| G G+ C | als vervanging van G7 C |
akkoorden • enharmonische verwisseling • gelijkzwevende stemming • fijnstemming • kerktoonsoorten • kwarttoon • kwintencirkel • liggend akkoord • maqam • polyfonie • theorie • tonaliteit • toonladder • transponeren
